Algorithmic Synth

General information

This Machine features 2 identical oscillators with 1216 modelsdifferent (thealgorithms number has changed with v1.1.3) toto choose from. Each oscillator can be tuned, transposed and have its own model.algorithm (model).

The oscillators go into a Filter section, then a Drive section and finally an Amp section before going to the Mixer.

Main screen of the algorithmic synth

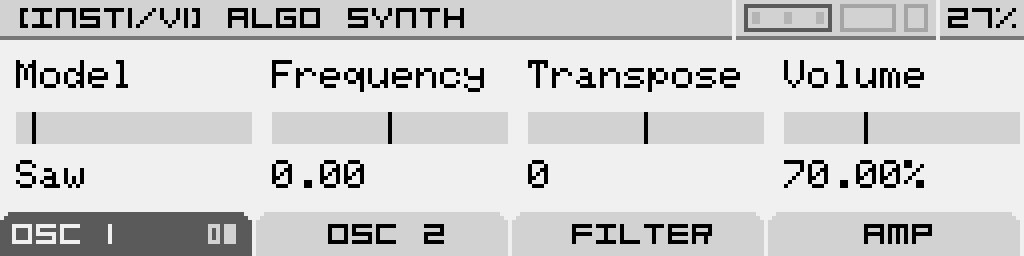
When opening the Algorithmic Synth Machine you will land on page 1 of tab 1. Use the first 2 tabs to configure oscillator 1 and 2 respectively. Use Tab 3 to configure the Filter section and Tab 4 to configure the Amp section.

The oscillator tabs (Tab 1 and Tab 2) will have a number of pages containing different controls depending on the selected model. When a Tab header displays small bar icons, click its corresponding button underneath to jump between its pages.

When you adjust a parameter on one the pages, a wave display is briefly shown to reflect the changes on the output wave. Click Button 4 while the wave display is shown to lock it on. Click Button 4 again to unlock the display.

The first page of an oscillator tab is always the same:

Model	Frequency	Transpose	Volume
Select the synthesis type used in the oscillator	Fine-tune the oscillator. This can be used to achieve beating-effects by having th two oscillators slightly out of tune with each other	Tune the oscillator by one semitone increments. This can be used to have the Machine play a paraphonic interval, or use one oscillator as a sub	Adjust the volume at which the oscillator is sent down the signal path (to the Filter section, or directly the the Amp section if all filters are turned off). 100% is unity gain, but it can go up to 200% if you can to overdrive the Filters, Amps or even the final DAC.

Saw model

A saw wave with SyncVirtual sync capabilities.
The oscillator tabs have 2 pages. Page 1 is the same as mentioned earlier.

Page 2:

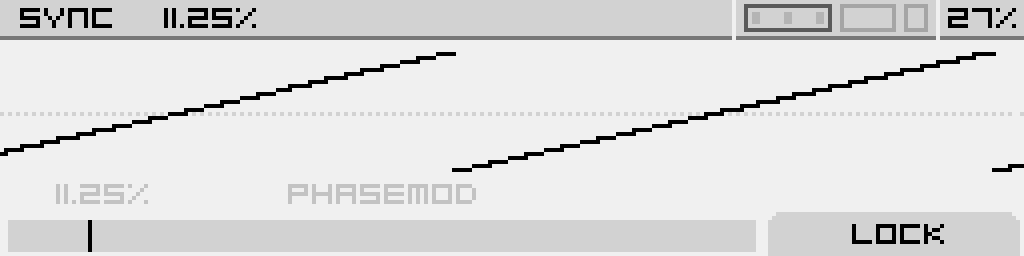
Sync	PhaseMod	-	-
Above 0%, the saw wave is synced to a master oscillator. This adjusts the frequency of the slave oscillator you're hearing. Modulate for classic sync sounds	Above 0%, the saw wave's phase is modulated by another oscillator tuned at 0.75 times the frequency of the Saw. Increasing the parameter augments the modulation depth	-	-

SuperSaw model

A swarm of detuned saw waves.
The oscillator tabs have 2 pages. Page 1 is the same as mentioned earlier.

Page 2:

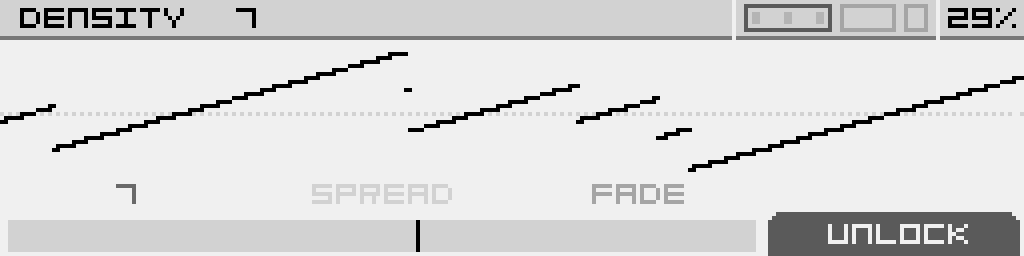
Density	Spread	Fade	-
Choose the number of saw waves in the swarm, up to 12	Adjust the amount of detuning between the waves	Apply a volume fade on the most detuned saw waves to make the output less chaotic	-

Square model

A Square wave with PWM capabilities.
The oscillator tabs have 2 pages. Page 1 is the same as mentioned earlier.

Page 2:

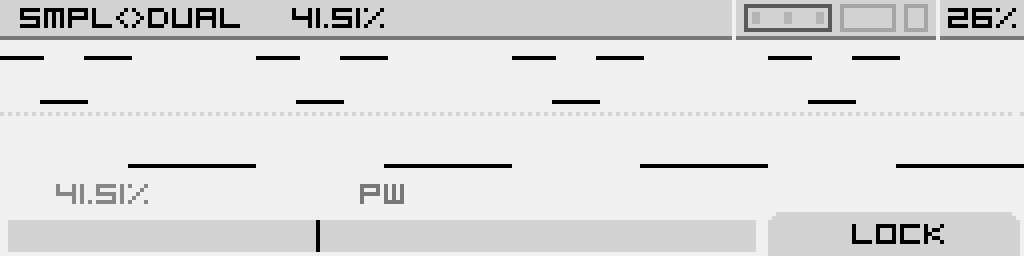
Simple<>Dual	PW	-	-
Add harmonics by dividing the positive part of the pulse in three pulse segments	Adjust the pulse-width of the output wave. Modulate for classic PWM sounds	-	-

Fold1 model

A sine wave is folded using the Chebyshev method
The oscillator tabs have 2 pages. Page 1 is the same as mentioned earlier.

Page 2:

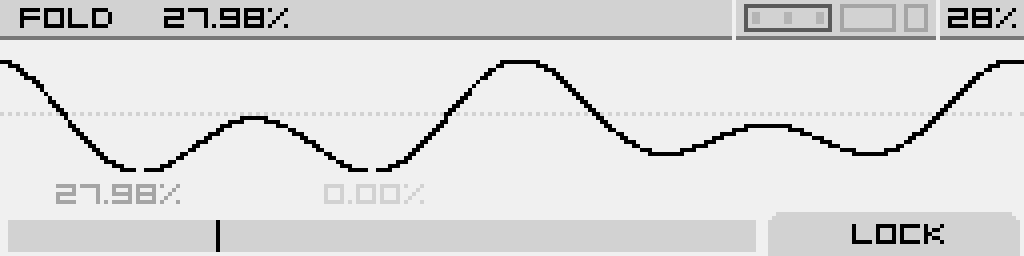
Fold	Decimator	-	-
Increase the number of folds in the wave to add harmonics.	Reduces the bit rate to add harmonics	-	-

Fold2 model

Two different out-of-phase waves are folded using the sinusoidal fold method
The oscillator tabs have 2 pages. Page 1 is the same as mentioned earlier.

Page 2:

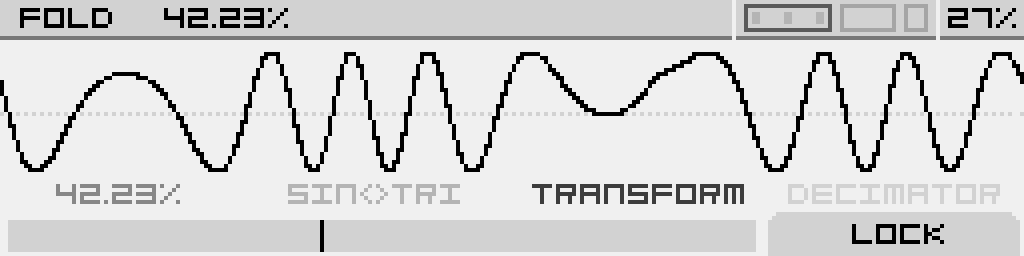
Fold	Sine<>Triangle	Transform	Decimator
Increase the number of folds in the wave to add harmonics.	Crossfade between a sine and a triangle wave, which are out-of-phase with each other	Adjust the phase of the sine and skew the triangle	Reduces the bit rate to add harmonics

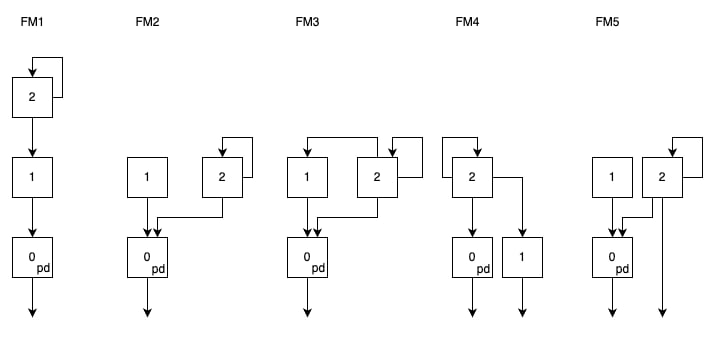
FM1 to FM8 model

A 3-op cascading4-Ops FM algorithm.algorithms.

You will find a diagram of the different FM algorithms at the end of this section.

Each algorithm has its own configuration, but it shares some common features :

• There is always 2 outputs from different operators (A/B), you can mix these 2 outputs
• All operators are sine oscillators, but the operator 1 has a phase distortion to twist the sine, this allows you to add more harmonics / harshness to the sound
• Each algorithm has 4 different modulation mode : TZFM Linear 1, TZFM Linear 2, Linear, Exponential.
• You can adjust the ratio / depth of each operator
• There is no integrated enveloppes on operators, but you can modulate every parameters with internal or external enveloppes (or other modulations) 

 

The oscillator tabs have 2 pages. Page 1 is the same as mentioned earlier.

Page 2:

Depth Op1	Ratio Op1	Depth Op2	Ratio Op2
Amount at which Operator 1 modulates the Carrier frequency	Adjust Operator 1 frequency, in multiples of the Carrier frequency	Amount at which Operator 2 modulates the frequency of Operator 1	Adjust Operator 2 frequency, in multiples of the Carrier frequency

Page 3:

Offset Op1	Offset Op2	Feedback	PhaseDist
Detune Operator 1 frequency ratio in small increments. Useful for inharmonic timbres and beating effects.	Detune Operator 2 frequency ratio in small increments. Useful for inharmonic timbres and beating effects.	Amount at which Operator 2 modulates it own frequency	Alter the shape of the Carrier sinewave. Below 50% it expands the duration of the negative part of the cycle and shrinks the positive part, above 50% it expands the positive part and shrinks the negative part.

FM2

FM model

Algorithms

A 3-op parallel FM algorithm.
You will find a diagram of the different FM algorithms at the end of this section.
The oscillator tabs have 2 pages. Page 1 is the same as mentioned earlier.

Page 2:

Depth Op1	Ratio Op1	Depth Op2	Ratio Op2
Amount at which Operator 1 modulates the Carrier frequency	Adjust Operator 1 frequency, in multiples of the Carrier frequency	Amount at which Operator 2 modulates the Carrier frequency	Adjust Operator 2 frequency, in multiples of the Carrier frequency

Page 3:

Offset Op1	Offset Op2	Feedback	PhaseDist
Detune Operator 1 frequency ratio in small increments. Useful for inharmonic timbres and beating effects.	Detune Operator 2 frequency ratio in small increments. Useful for inharmonic timbres and beating effects.	Amount at which Operator 2 modulates it own frequency	Alter the shape of the Carrier sinewave. Below 50% it expands the duration of the negative part of the cycle and shrinks the positive part, above 50% it expands the positive part and shrinks the negative part.

FM3 model

A 3-op FM algorithm with Operator 2 modulating both Operator 1 and the Carrier.
You will find a diagram of the different FM algorithms at the end of this section.
The oscillator tabs have 3 pages. Page 1 is the same as mentioned earlier.

Page 2:

Depth Op1	Ratio Op1	Depth Op2	Ratio Op2
Amount at which Operator 1 modulates the Carrier frequency	Adjust Operator 1 frequency, in multiples of the Carrier frequency	Amount at which Operator 2 modulates both Operator 1 and the Carrier	Adjust Operator 2 frequency, in multiples of the Carrier frequency

Page 3:

Offset Op1	Offset Op2	Feedback	PhaseDist
Detune Operator 1 frequency ratio in small increments. Useful for inharmonic timbres and beating effects.	Detune Operator 2 frequency ratio in small increments. Useful for inharmonic timbres and beating effects.	Amount at which Operator 2 modulates it own frequency	Alter the shape of the Carrier sinewave. Below 50% it expands the duration of the negative part of the cycle and shrinks the positive part, above 50% it expands the positive part and shrinks the negative part.

FM4 model

A 3-op FM algorithm with Operator 2 modulating both Operator 1 and the Carrier, and Operator 1 also audible as a Carrier.
You will find a diagram of the different FM algorithms at the end of this section.
The oscillator tabs have 3 pages. Page 1 is the same as mentioned earlier.

Page 2:

Depth Op1	Ratio Op1	Depth Op2	Ratio Op2
Amount at which Operator 1 modulates the Carrier frequency	Adjust Operator 1 frequency, in multiples of the Carrier frequency	Amount at which Operator 2 modulates both Operator 1 and the Carrier	Adjust Operator 2 frequency, in multiples of the Carrier frequency

Page 3:

Offset Op1	Offset Op2	Feedback	PhaseDist
Detune Operator 1 frequency ratio in small increments. Useful for inharmonic timbres and beating effects.	Detune Operator 2 frequency ratio in small increments. Useful for inharmonic timbres and beating effects.	Amount at which Operator 2 modulates it own frequency	Alter the shape of the Carrier sinewave. Below 50% it expands the duration of the negative part of the cycle and shrinks the positive part, above 50% it expands the positive part and shrinks the negative part.

FM5 model

A 3-op parallel FM algorithm with Operator 2 also audible as a Carrier.
You will find a diagram of the different FM algorithms at the end of this section.
The oscillator tabs have 3 pages. Page 1 is the same as mentioned earlier.

Page 2:

Depth Op1	Ratio Op1	Depth Op2	Ratio Op2
Amount at which Operator 1 modulates the Carrier frequency	Adjust Operator 1 frequency, in multiples of the Carrier frequency	Amount at which Operator 2 modulates the Carrier frequency	Adjust Operator 2 frequency, in multiples of the Carrier frequency

Page 3:

Offset Op1	Offset Op2	Feedback	PhaseDist
Detune Operator 1 frequency ratio in small increments. Useful for inharmonic timbres and beating effects.	Detune Operator 2 frequency ratio in small increments. Useful for inharmonic timbres and beating effects.	Amount at which Operator 2 modulates it own frequency	Alter the shape of the Carrier sinewave. Below 50% it expands the duration of the negative part of the cycle and shrinks the positive part, above 50% it expands the positive part and shrinks the negative part.

FM algorithms reference diagram

Ringmod model

Two Ring Modulation algorithms where one oscillator's frequency is a multiple of the other one.
Algorithm A is a Saturated Ring Modulation and algorithm B is more like a Diode-Based Ring Modulation.
The oscillator tabs have 2 pages. Page 1 is the same as mentioned earlier.

Page 2:

Ratio	Strength	Twist	Timbre
Select the modulator frequency, being a multiple of the carrier frequency.	Non-linear gain of both the carrier and modulator signals	Distort the phase of the modulator oscillator	Morph from algorithm A to algorithm B

CZ model

A phase modulation and wave windowing algorithm inspired by the Casio CZ series.
The oscillator tabs have 2 pages. Page 1 is the same as mentioned earlier.

Page 2:

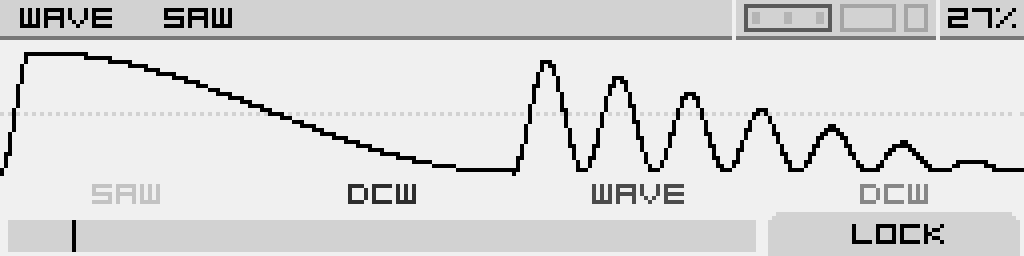
Wave	DCW	Wave	DCW
Select a target wave. If the second Wave parameter is not OFF, then this one will select a target wave for every odd cycle of the main sine.	Simulates a filter sweep by using a different phase modulation on each wave (combined with windowing on the Reso1, 2 and3 waves). At 0% only the main sine is heard, and at 100% only the target wave is heard.	Select a target wave for every even cycle of the main sine.	Simulates a filter sweep by using a different phase modulation on each wave (combined with windowing on the Reso1, 2 and3 waves). At 0% only the main sine is heard, and at 100% only the target wave is heard.